Séries e Sequências
SEQUÊNCIAS
Definição: Uma sequência é uma função cujo domínio é o conjunto dos números inteiros positivos. O contradomínio de uma sequência será considerado o conjunto dos números reais.
A cada número inteiro positivo "n" corresponde um número real f(n).
a1 = f(1) ; a2 = f(2) ; a3 = f(3) ; ... ; an = f(n)
Notações:
{an} = {a1, a2, a3, ..., an, ...}
an é o termo genérico da sequência.
Exemplos:
1) 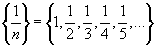
2) 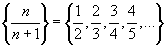
Se, quando n cresce, an se torna cada vez mais próximo de um número real L, diz-se que a sequência {an} tem limite L (ou converge para L) e se escreve:
Uma sequência que não é convergente, é chamada de divergente.
TEOREMA DO SANDUÍCHE
Se {an}, {bn}, {cn} são sequências tais que an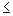 bn
bn 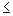 cn para todo
cn para todo 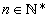 e se
e se
Se {an}, {bn}, {cn} são sequências tais que an
então 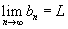
SÉRIES
Definição: Se {an} é uma sequência, então:
A soma infinita a1 + a2 + a3 + ... + an + ... = 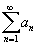 é chamada série.
é chamada série.
Cada número ai é um termo da série;
an é o termo genérico de ordem n.
Para definir a SOMA de infinitas parcelas, consideram-se as SOMAS PARCIAIS.
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
------------------------
Sn = a1 + a2 + a3 + ... + an-1 + an
E a SEQUÊNCIA DAS SOMAS PARCIAIS
S1, S2, S3, ..., Sn, ...
Se essa sequência tem limite S, então a série CONVERGE e sua soma é S.
Ou seja: Se 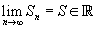 , então a série converge e sua soma é a1+a2+a3+...+an... = S
, então a série converge e sua soma é a1+a2+a3+...+an... = S
Se a sequência {Sn} não tem limite, então a série DIVERGE.
TEOREMA
Se a série 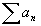 converge, então
converge, então 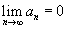
OBS: * A recíproca desse teorema é falsa, isto é, existem séries cujo termo genérico tende a zero e que não são convergentes.
* Vale a contrapositiva: "se o limite não é zero, então a série não converge", que constitui o:
| TESTE DA DIVERGÊNCIADada a série |
SÉRIE GEOMÉTRICA
TIPO: 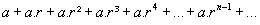 com a
com a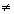 0
0
r é a razão.
Ex: 1 + 2 + 4 + 8 + 16 + ...
a = 1
r = 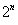
SOMA DE UMA SÉRIE GEOMÉTRICA
A série geométrica 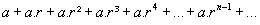
Converge e tem soma 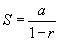 se | r | < 1.
se | r | < 1.
Diverge se | r | 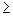 1.
1.
TESTE DA COMPARAÇÃO
Sejam 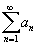 e
e 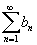 duas séries de termos positivos. Então:
duas séries de termos positivos. Então:
* Se 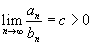 , sendo "c" um número real, então as séries são ambas convergentes ouambas divergentes.
, sendo "c" um número real, então as séries são ambas convergentes ouambas divergentes.
* Se 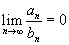 e se
e se 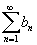 converge, então
converge, então 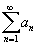 também converge.
também converge.
* Se 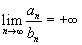 e se
e se 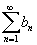 diverge, então
diverge, então 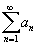 também diverge.
também diverge.
OBS: Se an é expressa por uma fração, devemos considerar tanto no numerador, quanto no denominador de bn somente os termos de maior importância.
Ex: Verifique se a série dada converge ou diverge:
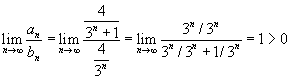
Logo, conclui-se que a série CONVERGE.
SÉRIE-P
CONVERGE se p > 1
DIVERGE se p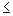 1
1
Se p = 1, a série
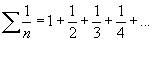 é chamada SÉRIE HARMÔNICA e, de acordo com o teorema, é divergente.
é chamada SÉRIE HARMÔNICA e, de acordo com o teorema, é divergente.
SÉRIE ALTERNADA
É da forma:
SÉRIES DE POTÊNCIA
Séries de potências de x:
ou
Séries de potência de (x-c):
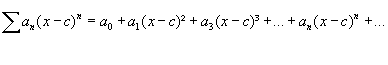
Por conveniência, vamos admitir que 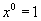 , mesmo quando x = 0.
, mesmo quando x = 0.
Ao substituir x por um número real, obtém-se uma série de termos constantes que pode convergir ou divergir.
Em qualquer série de potências de x, a série converge sempre para x=0, pois se substituirmos x por0 a série se reduz a a0.
Na série de potências de (x-c), a série converge para x = c.
Para determinar os outros valores de x para os quais a série converge, utiliza-se o teste da razão.
TESTE DE LEIBINZ
Uma série alternada CONVERGE se:
* Seu termo genérico, em módulo, tende a zero.
* A série dos módulos é decrescente.
Há três maneiras diferentes de verificar se a série dos módulos é decrescente.
a) verificar se, para todo "k" inteiro positivo, 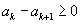 .
.
b) verificar se, para todo "k" inteiro positivo, 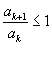 .
.
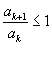 .
.
c) considerar a função f(x) = f(n) e verificar o sinal de sua derivada. Se f'(x)<0, então f é decrescente.
CONVERGÊNCIA ABSOLUTA
Definição: Uma série 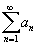 é absolutamente convergente se a série dos módulos
é absolutamente convergente se a série dos módulos
Ex: A série alternada 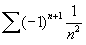 é absolutamente convergente, pois a série dos módulos
é absolutamente convergente, pois a série dos módulos 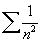 é uma série-p, com p=2 > 1 e, portanto, convergente.
é uma série-p, com p=2 > 1 e, portanto, convergente.
TEOREMA
Se uma série infinita 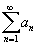 é absolutamente convergente, então a série é convergente.
é absolutamente convergente, então a série é convergente.
TESTE DE D'ALEMBERT
Seja 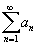 uma série de termos não nulos e seja
uma série de termos não nulos e seja 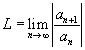 . Então:
. Então:
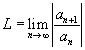 . Então:
. Então:
* Se L < 1, a série é ABSOLUTAMENTE CONVERGENTE.
* Se L > 1, (incluindo L = 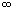 ), a série é DIVERGENTE.
), a série é DIVERGENTE.
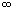 ), a série é DIVERGENTE.
), a série é DIVERGENTE.
* Se L = 1, o teste falha (nada se pode afirmar).
RESUMO
TESTE
|
SÉRIE
|
CONVERGÊNCIA ou DIVERGÊNCIA
|
COMENTÁRIOS
|
| daDIVERGÊNCIAou do N-ÉSIMO TERMO | DIVERGE se | Nada se pode afirmar se | |
| SÉRIE GEOMÉTRICA | * CONVERGE e tem soma | Útil para testes de comparação | |
| SÉRIE-P | * CONVERGE se p > 1* DIVERGE se p | Útil para testes de comparação | |
| daCOMPARAÇÃOno limite | * Se * Se | A série de comparação | |
| de LEIBNIZ | ALTERNADA an > 0 | CONVERGE se:* * A série | Aplicável somente a séries alternadas.Se o primeiro item é falso, aplica-se o TESTE DA DIVERGÊNCIA. |
Nenhum comentário:
Postar um comentário